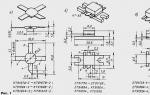
Как перевести в 5 систему счисления. Перевод чисел в различные системы счислений. Правила перевода чисел из любой системы счисления в десятичную

Коммивояжер (бродячий торговец) желает посетить ряд городов и вернуться в исходный город, минимизируя суммарную длину (стоимость) переездов. Эта задача в математической форме формулируется как задача нахождения во взвешенном графе гамильтонова цикла минимальной длины и называется задачей коммивояжера.

В качестве её практического приложения можно указать следующее. Пусть имеется станок, способный выполнять несколько операций. Его перенастройка с одной операции на другую требует определенных затрат. Требуется использовать станок в циклическом режиме, минимизируя суммарные затраты на перенастройку.

В данной задаче перенастройка с одной операции на другую и обратная перенастройка могут требовать, вообще говоря, различных затрат. Поэтому и в общем случае в задаче коммивояжера рассматривается взвешенный ориентированный граф, дуги которого в прямом и обратном направлении могут иметь различные веса.

Для решения задачи коммивояжера можно попытаться использовать «жадный алгоритм», успешно примененный в задаче о минимальном остовном дереве. Упорядочим предварительно дуги по весам и будем включать дуги минимального веса, следя за тем, чтобы не возникли вершины, полустепень исхода или захода которых превышает единицу, и не появились негамильтоновы циклы. Однако, как легко убедиться, данный подход не гарантирует получение оптимального решения. В качестве простейшего контрпримера можно рассмотреть следующий граф.

Здесь каждому ребру соответствует две дуги такого же веса.

«Жадный алгоритм» прежде всего включит в цикл ребро
, как имеющее минимальный вес. Включение этого ребра, как непосредственно легко проверить, необходимо ведет к гамильтонову циклу
веса 29. Оптимальный

же гамильтонов цикл
имеет вес 12. Поэтому «жадный алгоритм» не гарантирует получения оптимального решения, хотя он может быть использован на практике в качестве полезной эвристики, во многих случаях приводящей к решениям, близким к оптимальным.

Для задачи коммивояжера не известно какого – либо эффективного алгоритма. Весьма вероятно, что такого алгоритма не существует, хотя это и не удалось до сих пор доказать. Подобные задачи не редки в дискретной математике. В случае небольшой размерности их точные решения удается получать на компьютере с помощью метода «ветвей и границ».

Под методом «ветвей и границ» понимается широкий класс методов сокращенного перебора, суть которых сводится к следующему. Множество допустимых решений А разбивается на два подмножества А 0 и А 1 , затем каждое из подмножеств также разбивается на два подмножества и т.д. Схематически это можно представить в виде дерева, начинающегося с множества всех решений и заканчивающегося его одноэлементными подмножествами, т.е. допустимыми решениями, которыми в нашем случае являются гамильтоновы циклы.

Среди допустимых решений выбирается оптимальное по функционалу качества, которым в нашем случае является длина гамильтонова цикла. Смысл метода «ветвей и границ» состоит, однако, в том, чтобы не просматривать все допустимые решения, а отсекать большинство ветвей на возможно более раннем этапе. Для этого с помощью эвристических соображений стараются сразу пойти по ветви, ведущей к решению, близкому по качеству к оптимальному. После этого большинство других ветвей отсекают с помощью границ для функционала качества, когда удается показать, что в подмножестве решений не содержится решения, лучшего по качеству, чем уже имеющееся.

Рассмотрим метод «ветвей и границ» на примере задачи коммивояжера. Пусть взвешенный орграф задан матрицей расстояний. Если некоторая дуга в графе отсутствует, то соответствующий элемент матрицы будем полагать равным ∞. Заметим, что если длины всех дуг, входящих в некоторую вершину, уменьшить на одно и то же число, то и длина оптимального гамильтонова цикла уменьшится на это же число. То же самое относится и к множеству выходящих дуг. Будем последовательно вычитать из строк и столбцов матрицы расстояний положительные числа так, чтобы элементы матрицы оставались неотрицательными. Так как длина оптимального гамильтонова цикла для графа с неотрицательной матрицей расстояний также неотрицательна, то сумма вычтенных количеств будет нижней границей для длины оптимального цикла исходного графа.

Рассмотрим пример. Пусть задан граф G с симметрической матрицей расстояний.

Значки « ∞ » на диагонали соответствуют отсутствию в графе петель – дуг, ведущих из вершины в эту же вершину. Получим, прежде всего, нижнюю границу для длины кратчайшего гамильтонового цикла. Из первой, второй, третьей и четвертой строк можно вычесть по единице, из пятой строки – два, а из пятого столбца можно вычесть ещё единицу. Это дает нижнюю границу 7, а матрица расстояний приобретает вид

Теперь выберем дугу для ветвления, т.е. разобьем множество гамильтоновых циклов на два подмножества: включающих и не включающих эту дугу. Мы рассчитываем, что данная дуга будет входить в оптимальный или близкий к оптимальному цикл. Для этого будем следовать следующему эвристическому правилу: из множества дуг нулевой длины выбирать ту, исключение которой ведет к максимальному росту нижней оценки. В нашем случае такой дугой является дуга (1,2). Запрещение этой дуги приводит к матрице

из первой строки и второго столбца которой можно вычесть по единице, что увеличивает нижнюю границу на 2 и делает её равной 9.

Включение же дуги (1,2) приводит к тому, что исключаются все остальные дуги, ведущие в вершину 2, и все остальные дуги, выходящие из вершины 1. Поэтому первую строку и второй столбец матрицы можно далее не рассматривать, и они вычеркиваются из матрицы. Кроме того, исключается дуга (2,1). Матрица принимает вид

Из её первой строки и первого столбца можно вычесть по единице, что приводит к матрице

Нижняя оценка здесь возрастает на 2 и также становится равной 9.

Нижняя оценка длины оптимального цикла остается неизменной.

Дуга (2,5) должна быть запрещена, как ведущая к появлению негамильтонова цикла, и матрица принимает вид

Нижняя оценка длины гамильтонова цикла остается, по – прежнему, равной 9.

Схематически представим проведенный анализ в виде дерева, где в кружочках стоят нижние оценки длины гамильтонова цикла.

Взглянув на это дерево, непосредственно убеждаемся, что полученный гамильтонов цикл является кратчайшим, т.к. движение по любой другой ветви дерева не может привести к более короткому циклу.

Существует ли эффективный алгоритм для решения задачи коммивояжера? а) да; б) нет; в) неизвестно.

Является ли описанный метод « ветвей и границ» эффективным алгоритмом для решения задачи коммивояжера? а) да; б) нет; в) неизвестно.

Здравствуй, Хабр! Реализовывая различные алгоритмы для нахождения гамильтонова цикла с наименьшей стоимостью, я наткнулся на публикацию , предлагающую свой вариант. Попробовав в деле, я получил неправильный ответ:

Дальнейшие поиски в Интернете не принесли ожидаемого результата: либо сложное для не-математиков теоретическое описание, либо понятное, но с ошибками.

Под катом вас будет ждать исправленный алгоритм и онлайн-калькулятор.

Сам метод, опубликованный Литтлом, Мерти, Суини, Кэрелом в 1963 г. применим ко многим NP-полным задачам, и представляет собой очень теоритеризованный материал, который без хороших знаний английского языка и математики сразу не применишь к нашей задаче коммивояжера.

Кратко о методе - это полный перебор всех возможных вариантов с отсеиванием явно неоптимальных решений.

Исправленный алгоритм, для нахождения действительно минимального маршрута

Алгоритм состоит из двух этапов:

Первый этап

Приведение матрицы затрат и вычисление нижней оценки стоимости маршрута r.

Второй (основной) этап

А) Ищем все нулевые элементы в приведенной матрице
б) Для каждого из них считаем его штраф за неиспользование.
в) Выбираем элемент, которому соответствует максимальный штраф (любой, если их несколько)

2. Теперь наше множество S разбиваем на множества - содержащие ребро с максимальным штрафом(S w) и не содержащие это ребро(S w/o).
3. Вычисление оценок затрат для маршрутов, входящих в каждое из этих множеств.
а) Для множества S w/o все просто: раз мы не берем соответствующее ребро c максимальным штрафом(h,k), то для него оценка затрат равна оценки затрат множества S + штраф за неиспользование ребра (h,k)
б) При вычислении затрат для множества S w примем во внимание, что раз ребро (h,k) входит в маршрут, то значит ребро (k,h) в маршрут входить не может, поэтому в матрице затрат пишем c(k,h)=infinity, а так как из пункта h мы «уже ушли», а в пункт k мы «уже пришли», то ни одно ребро, выходящее из h, и ни одно ребро, приходящее в k, уже использоваться не могут, поэтому вычеркиваем из матрицы затрат строку h и столбец k. После этого приводим матрицу, и тогда оценка затрат для S w равна сумме оценки затрат для S и r(h,k), где r(h,k) - сумма констант приведения для измененной матрицы затрат.
4. Из всех неразбитых множеств выбирается то, которое имеет наименьшую оценку.

Так продолжаем, пока в матрице затрат не останется одна не вычеркнутая строка и один не вычеркнутый столбец.

Небольшая оптимизация - подключаем эвристику

Да, правда, почему бы нам не ввести эвристику? Ведь в алгоритме ветвей и границ мы фактически строим дерево, в узлах которого решаем брать ребро (h,k) или нет, и вешаем двух детей - Sw(h,k) и Sw/o(h,k). Но лучший вариант для следующей итерации выбираем только по оценке. Так давайте выбирать лучший не только по оценке, но и по глубине в дереве, т.к. чем глубже выбранный элемент, тем ближе он к концу подсчета. Тем самым мы сможем наконец дождаться ответа.

Теперь, собственно, об ошибках в той публикации

Доказательство

Вернемся к картинке в начале поста:

Ответ: путь:3=>4=>2=>1=>5=>3 длина: 41
Как видите, включая ребро 5:2 в решение будет ошибкой. Что и требовалось доказать

График сравнения метода ветвей и границ и потраченного времени для случайной таблицы от 5х5 до 10х10:


График максимального и минимального потраченного времени для матриц от 5х5 до 66х66.


Попробовать с подробным решением можно

Впервые метод ветвей и границ был предложен в 1960 г. в работе Лэнд и Дойг применительно к задаче целочисленного линейного программирования. Однако эта работа не оказала заметного непосредственного влияния на развитие дискретного программирования. Фактически «второе рождение» метода ветвей и границ связано с работой Литтла, Мурти, Суини и Кэрел , посвященной задаче коммивояжера; в этой же работе было впервые предложено и общепринятое теперь название метода «метод ветвей и границ». Начиная с этого момента появляется весьма большое число работ, посвященных методу ветвей и границ и различным его модификациям. Столь большой успех (да еще применительно к «классически трудной» задаче о коммивояжере) объясняется тем, что Литтл, Мурти, Суини и Кэрел первыми обратили внимание на широту возможностей метода ветвей и границ, отметили важность использования специфики задачи и сами весьма удачно этой спецификой воспользовались.

В § 1 настоящей главы излагается общая идея метода ветвей и границ; в § 2 - алгоритм Лэнд и Дойг для задачи целочисленного линейного программирования, в § 3 - метод Литтла и др. авторов для задачи коммивояжера.

§ 1. Идея метода ветвей и границ

1.1. Рассмотрим задачу дискретного программирования в следующей общей форме.

Минимизировать

при условии

Здесь G - некоторое конечное множество.

1.2. В основе метода ветвей и границ лежат следующие построения, позволяющие в ряде случаев существенно уменьшить объем перебора.

I. Вычисление нижней границы (оценки).

Часто удается найти нижнюю границу (оценку) целевой функции на множестве планов (или на некотором его подмножестве т. е. такое число что для имеет место

(соответственно для имеет место Разбиение на подмножества (ветвление). Реализация метода связана с постепенным разбиением множества планов на дерево подмножеств (ветвлением). Ветвление происходит по следующей многошаговой схеме.

0-й шаг. Имеется множество Некоторым способом оно разбивается на конечное число (обычно не пересекающихся) подмножестве шаг Имеются множества , еще не подвергавгпиеся ветвлению. По некоторому правилу (указанному ниже) среди них выбирается множество и разбивается на конечное число подмножеств:

Еще не подвергавшиеся разбиению множества

заново обозначаются через

Несколько шагов такого процесса последовательного разбиения схематически изображены на рис. 10.1.1.

III. Пересчет оценок. Если множество то, очевидно,

Поэтому, разбивая в процессе решения некоторое множество на подмножества

В конкретных ситуациях часто оказывается возможным добиться улучшения оценки, т. е. получить хотя бы для некоторых строгое неравенство

IV. Вычисление планов. Для конкретных задач могут быть указаны различные способы нахождения планов в последовательно разветвляемых подмножествах. Любой такой способ существенно опирается на специфику задачи.

V. Признак оптимальности. Пусть

и план X принадлежит некоторому подмножеству Если при этом

то X - оптимальный план задачи (1.1) - (1.2).

Доказательство непосредственно следует из определения оценки.

Обычно этот признак применяется на некотором этапе ветвления (т. е., говоря формально, при ; см. п. II).

VI. Оценка точности приближенного решения. Пусть

Если X - некоторый план исходной задачи (т. е. ), то

Доказательство и здесь сразу следует из определения оценки.

Очевидно, что если разность невелика (т. е. не превышает некоторого выбранного для данной задачи числа), то X можно принять за приближенное решение, за оценку точности приближения.

1.3. Изложим формальную схему метода ветвей и границ.

0-й шаг. Вычисляем оценку . Если при этом удается найти такой план X, что

то X - оптимальный план.

Если оптимальный план не найден, то по некоторому способу разбиваем множество на конечное число подмножеств

и переходим к шагу.

1-й шаг. Вычисляем оценки Если при этом удается найти такой план X, что для некоторого и

то X - оптимальный план.

Если же оптимальный план не найден, то выбираем «наиболее перспективное» для дальнейшего разбиения множество по следующему правилу:

Разбиваем множество на несколько (обычно не пересекающихся) подмножеств.